Задание № 198 

Сложность: II
Классификатор алгебры: 3\.11\. Иррациональные уравнения
Иррациональные уравнения
i
Сумма корней (корень, если он единственный) уравнения 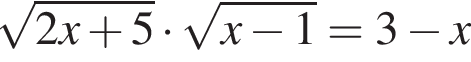 равна (равен):
равна (равен):
1) 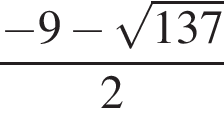
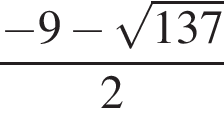
2) 
3) 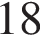
4) 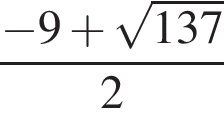
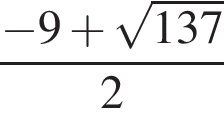
5) 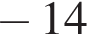
Решение. Найдем все возможные значения переменной:
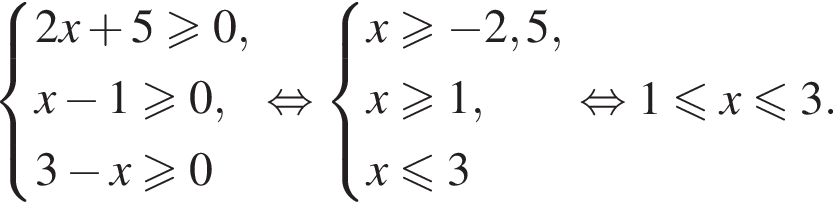
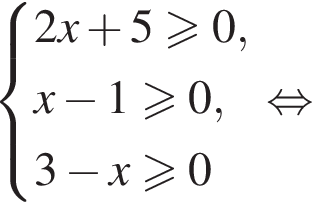
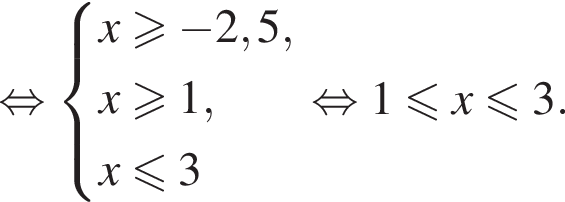
Возведем правую и левую части в квадрат на отрезке [1;3]:
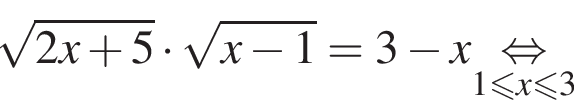
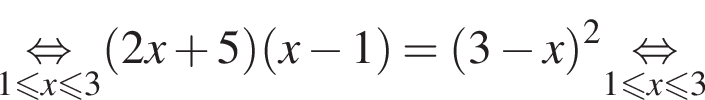
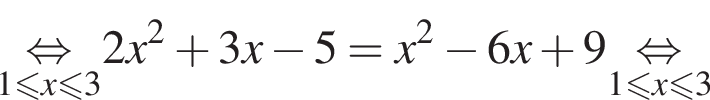
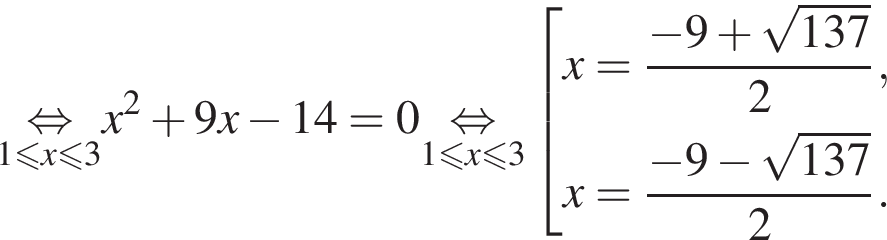
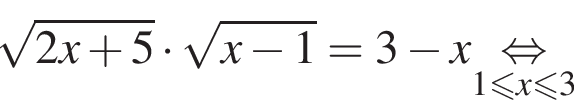
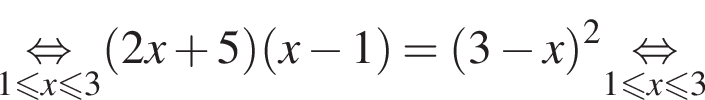
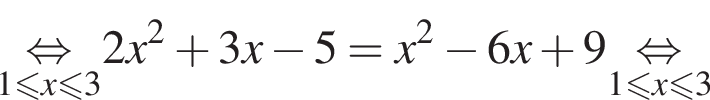
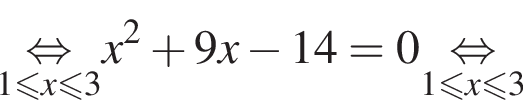
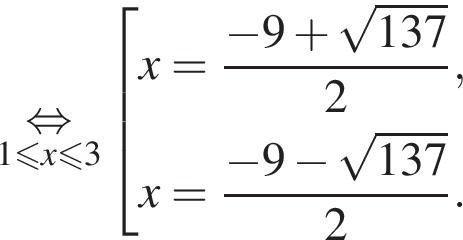
Число 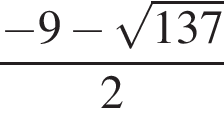 не лежит на отрезке [1;3]. Число
не лежит на отрезке [1;3]. Число 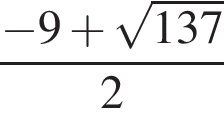 является решением уравнения в силу цепочки соотношений:
является решением уравнения в силу цепочки соотношений:
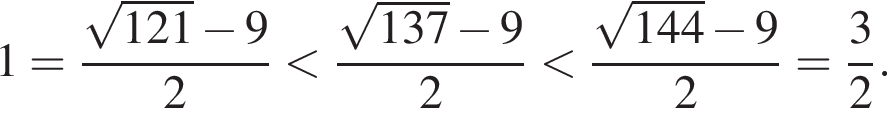
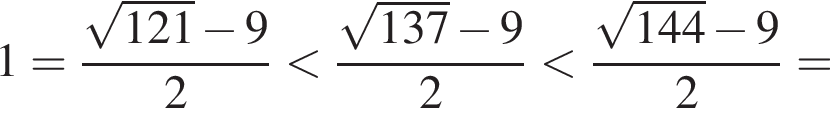
![]()
![]()
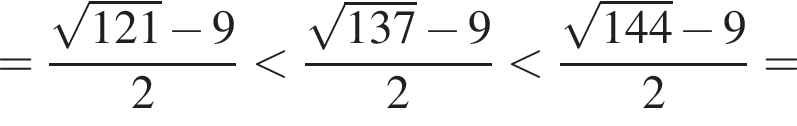
![]()
Правильный ответ указан под номером 4.
Ответ: 4
198
4
Сложность: II
Классификатор алгебры: 3\.11\. Иррациональные уравнения